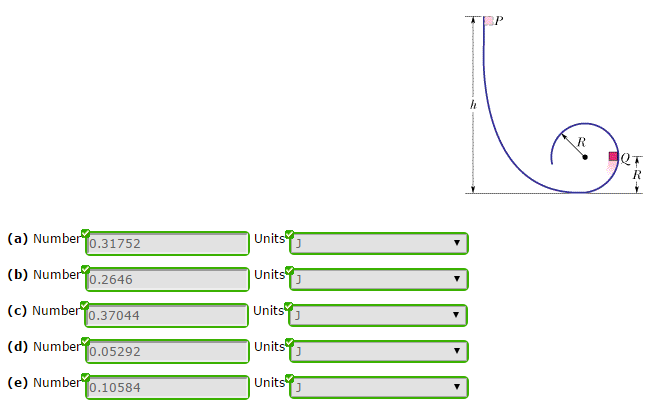
1. In the figure, a small block of mass m = 0.045 kg can slide along the frictionless loop-the-loop, with loop radius R = 12 cm. The block is released from rest at point P, at height h = 7Rabove the bottom of the loop. How much work does the gravitational force do on the block as the block travels from point P to (a) point Q and (b) the top of the loop? If the gravitational potential energy of the block-Earth system is taken to be zero at the bottom of the loop, what is that potential energy when the block is (c) at point P, (d) at point Q, and(e) at the top of the loop?
2. The figure shows an 8.3 kg stone at rest on a spring. The spring is compressed 11 cm by the stone. (a) What is the spring constant? (b) The stone is pushed down an additional 30 cm and released.What is the elastic potential energy of the compressed spring just before that release? (c) What is the change in the gravitational potential energy of the stone–Earth system when the stone moves from the release point to its maximum height? (d) What is that maximum height, measured from the release point?

3. The string in the figure is L = 117 cm long, has a ball attached to one end, and is fixed at its other end. The distance d from the fixed end to a fixed peg at point P is 79 cm. When the initially stationary ball is released with the string horizontal as shown, it will swing along the dashed arc. What is its speed when it reaches (a) its lowest point and (b) its highest point after the string catches on the peg?

4. Tarzan, who weighs 668 N, swings from a cliff at the end of a convenient vine that is 19 m long (see the figure). From the top of the cliff to the bottom of the swing, he descends by 2.2 m. The vine will break if the force on it exceeds 1280 N. What would the greatest force on the vine be during the swing?
882.6947 Units: N
5. A 2.1 kg breadbox on a frictionless incline of angle θ = 45 ˚ is connected, by a cord that runs over a pulley, to a light spring of spring constant k = 120 N/m, as shown in the figure. The box is released from rest when the spring is unstretched. Assume that the pulley is massless and frictionless. (a) What is the speed of the box when it has moved 10.6 cm down the incline? (b) How far down the incline from its point of release does the box slide before momentarily stopping, and what are the (c) magnitude and (d) direction of the box’s acceleration at the instant the box momentarily stops?

6. A rope is used to pull a 5.07 kg block at constant speed 6.75 m along a horizontal floor. The force on the block from the rope is 6.23 N and directed 33.0° above the horizontal. What are(a) the work done by the rope’s force, (b) the increase in thermal energy of the block-floor system, and (c) the coefficient of kinetic friction between the block and floor?

7. In the figure, a block slides down an incline. As it moves from point A to point B, which are 3.2 m apart, force acts on the block, with magnitude 2.9 N and directed down the incline. The magnitude of the frictional force acting on the block is 14 N. If the kinetic energy of the block increases by 34 J between A and B, how much work is done on the block by the gravitational force as the block moves from A to B?

8. A 4.3 kg bundle starts up a 27° incline with 107 J of kinetic energy. How far will it slide up the incline if the coefficient of kinetic friction between bundle and incline is 0.40?
3.1332 Units: m
9. The cable of the 2200 kg elevator cab in the figure snaps when the cab is at rest at the first floor, where the cab bottom is a distance d = 3.7 m above a spring of spring constant k = 0.29 MN/m. A safety device clamps the cab against guide rails so that a constant frictional force of 3.7 kN opposes the cab’s motion. (a) Find the speed of the cab just before it hits the spring. (b) Find the maximum distance x that the spring is compressed (the frictional force still acts during this compression). (c) Find the distance (above the point of maximum compression) that the cab will bounce back up the shaft. (d) Using conservation of energy, find the approximate total distance that the cab will move before coming to rest. (Assume that the frictional force on the cab is negligible when the cab is stationary.)

10. A conservative force F(x) acts on a 1.9 kg particle that moves along an x axis. The potential energy U(x) associated with F(x) is graphed in the figure. When the particle is at x = 2.0 m, its velocity is –1.6 m/s. (a) What is F(x) at this position, including sign? Between what positions on the (b) left and (c) right does the particle move? (d) What is its particle’s speed at x = 7.0 m?







