Click on the images to open a new tab and see them in full resolution.
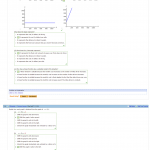
1. F(x) = 2(x-2)^2 g(x) = -1x^2 -2.5x+1
2. Find an expression for a cubic function f if f(3) = 24 and f(-1) = f(0) = f(4) = 0
Answer: f(x) = -2x(x+1)(x-4)
Find an expression for a cubic function f if f(3) = 72 and f(-1) = f(0) = f(4) = 0
Answer: f(x) = -6x(x+1)(x-4)
Find an expression for a cubic function f if f(1) = 8 and f(-1) = f(0) = f(2) = 0
Answer: f(x) = -4x(x+1)(x-2)
3. Some scientists believe that the average surface temperature of the world has been rising steadily. They have modeled the temperature by the linear function T = 0.01t + 8.55, where T is temperature in Celsius and t represents years since 1900.
(a)What do the slope an T-intercept represent
The slope is 0.01 which means that the average surface area temperature of the planet is increasing at a rate of 0.01 degree Celsius per year. The T-intercept is 8.55, which represents the average surface temperature in the year 1900.
(b) Use the equation to predict the average global surface temperature In 2030.
Answer: 9.85
Some scientists believe that the average surface temperature of the world has been rising steadily. They have modeled the temperature by the linear function T = 0.01t + 8.75, where T is temperature in Celsius and t represents years since 1900.
(a)What do the slope an T-intercept represent
The slope is 0.01 which means that the average surface area temperature of the planet is increasing at a rate of 0.01 degree Celsius per year. The T-intercept is 8.75, which represents the average surface temperature in the year 1900.
(b) Use the equation to predict the average global surface temperature In 2080.
Answer: 10.55
Some scientists believe that the average surface temperature of the world has been rising steadily. They have modeled the temperature by the linear function T = 0.01t + 8.75, where T is temperature in Celsius and t represents years since 1900.
(a)What do the slope an T-intercept represent
The slope is 0.01 which means that the average surface area temperature of the planet is increasing at a rate of 0.01 degree Celsius per year. The T-intercept is 8.75, which represents the average surface temperature in the year 1900.
(b) Use the equation to predict the average global surface temperature In 2010.
Answer: 9.85
4. The relationship between (f) and Celsius (c) temperature scales is given by the linear function F = 9C/5 + 32.
(b) What is the slope of the graph?
Answer: 9/5
What does it represent?
Answer: 9/5
What is the F-Intercept?
Answer: 32
What does it represent?
Answer 32
5. Jason leaves Detroit at 8:00 PM and drives at a constant speed west along I-96. He passes Ann Arbor, 40 mi from Detroit at 8:40 PM.
(a) Express the distance d traveled in terms of the time(in hours) elapsed.
Answer: 60t
(c) Answer 60
What does it represent? The slope represents the car’s speed in miles per hour.
Jason leaves Detroit at 9:00 PM and drives at a constant speed west along I-96. He passes Ann Arbor, 40 mi from Detroit at 9:40 PM.
(b) Express the distance d traveled in terms of the time(in hours) elapsed.
Answer: 60t
(c) Answer 60
What does it represent? The slope represents the car’s speed in miles per hour.
Jason leaves Detroit at 9:00 PM and drives at a constant speed west along I-96. He passes Ann Arbor, 40 mi from Detroit at 9:48 PM.
(c) Express the distance d traveled in terms of the time(in hours) elapsed.
Answer: 50t
(c) Answer 50
What does it represent? The slope represents the car’s speed in miles per hour.
6. Biologists have noticed that the chirping rate of crickets of certain species is related to temperature, and the relationship appears to be very nearly linear. A cricket produces 113 chirps per minute at 70 ° F and 183 chirps per minute at 80 °F
(a) Answer: 1N/7 + 377/7
(b) Answer: 1/7, degrees increase 1/7
This is the red #-160 chirps per minute
(c) Answer: 77
Biologists have noticed that the chirping rate of crickets of certain species is related to temperature, and the relationship appears to be very nearly linear. A cricket produces 113 chirps per minute at 70 ° F and 153 chirps per minute at 80 °F
(a) Answer: 1N/4 + 167/4
(b) Answer: 1/4, degrees increase 1/4
This is the red #-160 chirps per minute
(c) Answer: 82
If red number is #110 Answer: 69
7. The manager of a furniture factor finds that it costs $2200 to manufacture 70 chairs in one day and $4800 to produce 270 chairs in one day.
(a) Answer: 13x+1290
(b) Answer: 13
(c) Answer: 1290
The manager of a furniture factor finds that it costs $2200 to manufacture 90 chairs in one day and $4800 to produce 290 chairs in one day.
(d) Answer: 13x+1030
(e) Answer: 13
(f) Answer: 1030
The manager of a furniture factor finds that it costs $2000 to manufacture 90 chairs in one day and $4800 to produce 290 chairs in one day.
(g) Answer: 14x+740
(h) Answer: 14
(i) Answer: 740
8. At the surface of the ocean, the water pressure is the same of the air pressure above the water, 15lb/in^2. Below the surface, the water pressure increases by 4.34lb/in^2 for every 10 ft of descent.
(a) Answer: 15+ 0.434d
(b) 150 red # Answer: 311 120 red # Answer: 242
9. The monthly cost of driving a car depends on the number of miles driven. Lynn found that it costs her $345 to drive 300 mi and in June it cost her $475 to drive 820 mi.
(a) Answer: 0.25d+270
(b) 695
(c) It represents the cost in dollars per mile
(d) It represents the fixed cost
(e) A linear function is suitable because the monthly cost increases as the number of miles driven increases
The monthly cost of driving a car depends on the number of miles driven. Lynn found that it costs her $460 to drive 360 mi and in June it cost her $580 to drive 840 mi.
(a) Answer: 0.25d+370
(b) 845
(c) It represents the cost in dollars per mile
(d) It represents the fixed cost
(e) A linear function is suitable because the monthly cost increases as the number of miles driven increases
The monthly cost of driving a car depends on the number of miles driven. Lynn found that it costs her $385 to drive 460 mi and in June it cost her $435 to drive 660 mi.
(a) Answer: 0.25d+270
(b) 570
(c) It represents the cost in dollars per mile
(d) It represents the fixed cost
(e) A linear function is suitable because the monthly cost increases as the number of miles driven increases
10. Skipped
11. Skipped
12. Skipped
13. f(x) = x^3 +2x^2, g(x) = 4x^2 – 3
f+g = x^3 + 6x^2 – 3 Domain: (-infinity, infinity)
B. x^3 – 2x^2 + 3 domain: (-infinity, infinity)
c. 4x^5 + 8x^4 -3x^3 -6x^2 domain: (-infinity, infinity)
d. (x^3 + 2x^2)/ 4x^2 – 3) domain: (-infinity, -sqrt(3/4)U (-sqrt(3/4),sqrt(3/4)U(sqrt(3/4),infinity)
f(x) = x^3 +3x^2, g(x) = 7x^2 – 1
f+g = x^3 + 10x^2 – 1 Domain: (-infinity, infinity)
B. x^3 – 4x^2 + 1 domain: (-infinity, infinity)
c. 7x^5 + 21x^4 -x^3 -3x^2 domain: (-infinity, infinity)
d. (x^3 + 3x^2)/ 7x^2 – 1) domain: (-infinity, -sqrt(1/7)U (-sqrt(1/7),sqrt(1/7)U(sqrt(1/7),infinity)
f(x) = x^3 +3x^2, g(x) = 5x^2 – 2
f+g = x^3 + 8x^2 – 2 Domain: (-infinity, infinity)
B. x^3 – 2x^2 + 2 domain: (-infinity, infinity)
c. 5x^5 + 15x^4 -2x^3 -6x^2 domain: (-infinity, infinity)
d. (x^3 + 3x^2)/ 5x^2 – 2) domain: (-infinity, -sqrt(2/5)U (-sqrt(2/5),sqrt(2/5)U(sqrt(2/5),infinity)
14. f(x) = sqrt(5-x), g(x) = sqrt(x^2 – 4)
a. sqrt(5-x) + sqrt(x^2 -4) domain: (-infinity, -2]U[2,5]
b. sqrt(5-x) – sqrt(x^2-4) domain: (-infinity,-2)U[2,5]
c. sqrt(5-x) * sqrt(x^2 -4) domain: (-infinity, -2)U[2,5]
d. sqrt(5-x)/ sqrt(x^2-4) domain: (-infinity, -2) U(2,5]
f(x) = sqrt(4-x), g(x) = sqrt(x^2 -9)
a. sqrt(4-x) + sqrt(x^2 -9) domain: (-infinity, -3]U[3,4]
b. sqrt(4-x) – sqrt(x^2-9) domain: (-infinity,-3)U[3,4]
c. sqrt(4-x) * sqrt(x^2 -9) domain: (-infinity, -3)U[3,4]
d. sqrt(4-x)/ sqrt(x^2-9) domain: (-infinity, -3) U(3,4]
a. sqrt(5-x) + sqrt(x^2 -9) domain: (-infinity, -3]U[3,5]
b. sqrt(5-x) – sqrt(x^2-9) domain: (-infinity,-3)U[3,5]
c. sqrt(5-x) * sqrt(x^2 -9) domain: (-infinity, -3)U[3,5]
d. sqrt(5-x)/ sqrt(x^2-9) domain: (-infinity, -3) U(3,5]
15. f(x) = x^2 -1, g(x) = 2x+1
a. (2x+1)^2 -1 domain: (-infinity,infinity)
b. (2x^2 -1 ) domain: (-infinity,infinity)
c. (x^2 -1)^2 -1 domain: (-infinity,infinity)
d. (4x+3) domain: (-infinity,infinity)
f(x) = x^2 -2, g(x) = 2x+5
a. (2x+5)^2 domain: (-infinity,infinity)
b. 2(x^2-2) +5 domain: (-infinity,infinity)
c. (x^2-2)^2 -2 domain: (-infinity,infinity)
d. 2(2x+5) +5 domain: (-infinity,infinity)
f(x) x^2-2 , g(x) = 4x+3
a. (4x+3)^2 -2 domain: (-infinity,infinity)
b. 4x^2 – 5 domain: (-infinity,infinity)
c. x^4 -4x^2 +2 domain: (-infinity,infinity)
d. (16x +15) domain: (-infinity,infinity)