1. The figure shows a rigid structure consisting of a circular hoop of radius R and mass m, and a square made of four thin bars, each of length R and mass m. The rigid structure rotates at a constant speed about a vertical axis, with a period of rotation of 4.6 s. If R = 0.8 m and m = 2.9 kg, calculate the angular momentum about that axis.

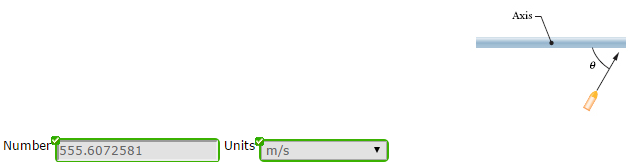
2. A uniform thin rod of length 0.26 m and mass 4.8 kg can rotate in a horizontal plane about a vertical axis through its center. The rod is at rest when a 3.9 g bullet traveling in the rotation plane is fired into one end of the rod. As viewed from above, the bullet’s path makes angle θ = 60° with the rod. If the bullet lodges in the rod and the angular velocity of the rod is 9.00 rad/s immediately after the collision, what is the bullet’s speed just before impact?
3. In the figure, a uniform sphere of mass m = 0.769 kg and radius r = 0.247 m is held in place by a massless rope attached to a frictionless wall a distance L = 2.10 m above the center of the sphere. Find (a) the tension in the rope and (b) the force on the sphere from the wall.

4. The system in the figure below is in equilibrium, with the string in the center exactly horizontal. Block A weighs 42.0 N, block B weighs 50.0 N, and angle φ is 32.0˚. What are
Find (a) tension T1, (b) tension T2, (c) tension T3, and (d) angle θ.

5. In the figure, what magnitude of force applied horizontally at the axle of the wheel is necessary to raise the wheel over an obstacle of height h = 0.165 m? The wheel’s radius is r= 0.615 m and its mass is m = 0.873 kg.

6. In the figure, suppose the length L of the uniform bar is 3.5 m and its weight is 160 N. Also, let the block’s weight W = 250 N and the angle θ = 39˚. The wire can withstand a maximum tension of 380 N. (a) What is the maximum possible distance x before the wire breaks? With the block placed at this maximum x, what are the (b) horizontal and (c)vertical
components of the force on the bar from the hinge at A?

7. In the figure, a 50.0 kg uniform square sign, of edge length L = 2.21 m, is hung from a horizontal rod of length dh = 3.28 m and negligible mass. A cable is attached to the end of the rod and to a point on the wall at distance dv = 4.96 m above the point where the rod is hinged to the wall. (a) What is the tension in the cable? (b) What is the horizontal component of the force on the rod from the wall? Take the positive direction to be to the right. (c) What is the vertical component of this force? Take the positive direction to be upward.

8. In the figure, the driver of a car on a horizontal road makes an emergency stop by applying the brakes so that all four wheels lock and skid along the road. The coefficient of kinetic friction between tires and road is 0.31. The separation between the front and rear axles is L = 4.5 m, and the center of mass of the car is located at distance d = 2.4 m behind the front axle and distance h = 1.1 m above the road. The car weighs 11 kN. Find the magnitude of (a) the braking acceleration of the car, (b) the normal force on each rear wheel, (c)the normal force on each front wheel, (d) the braking force on each rear wheel, and (e) the braking force on each front wheel. (Hint: Although the car is not in translational equilibrium, it is in rotational equilibrium.
9. For the stepladder shown in the figure, sides AC and CE are each 3.35 m long and hinged at C. Bar BD is a tie-rod 0.738 m long, halfway up. A man weighing 874 N climbs 2.51 m along the ladder. Assuming that the floor is frictionless and neglecting the mass of the ladder, find (a) the tension in the tie-rod and the magnitudes of the forces on the ladder from the floor at (b) A and (c) E. (Hint: Isolate parts of the ladder in applying the equilibrium conditions.)
10. Four bricks of length L, identical and uniform, are stacked on top of one another (the figure) in such a way that part of each extends beyond the one beneath. Find, in terms of L, the maximum values of (a) a1, (b) a2, (c) a3, (d) a4, and (e) h, such that the stack is in equilibrium.







